This is a particle-mesh n-body code for cosmological n-body simulations. This code has several uses.

• Testing new methods: For many methods of analysis in cosmology it can be very helpful to have a 2D sample available to test them with.
• Teaching: This code is very nice to play around with for students, since it is written in 100% Python.
• Learning: Lastly, having 2D simulations can give a great deal of insight.

Instructions

To run the code, you need to have installed:

• Python 3.8
• Numpy
• Scipy
• Gnuplot

Run with:

python -m nbody.nbody

License

Copyright 2015-2020 Johan Hidding; This code is licensed under the Apache license version 2.0, see LICENSE.

Citation

If you use this code in scientific publication, please cite it using DOI:10.5281/zenodo.4158731.

The math

It would be a bit much to derive all equations here from first principles. If you need a good introductory text, I recommend Barbara yden’s book “Introduction to Cosmology” (Ryden 2017) (link to PDF) The equations that gouvern the distribution of matter in the Universe are given by Newtons law for gravity. We assume gravity is the sole force responsible for forming strunctures in the Universe and that relativistic effects play a minor role. Moreover we will assume that this process is dominated by dark matter. The Newtonian field equation for gravity is the Poisson equation

\[\nabla^2 \Phi = 4 \pi G \rho.\](1)

However, in an expanding Universe this equation changes slightly to

\[\frac{1}{a^2} \nabla^2 \phi = 4 \pi G \rho_u \delta.\](2)

Here \(a\) is the Hubble expansion factor, \(\delta\) the density perturbation

\[\delta + 1 = \frac{\rho}{\rho_u},\](3)

and \(\phi\) is the potential perturbation. Similarly the Euler equation describing Newton’s second law can be written in Lagrangian form as

\[\partial_t(a \vec{v}) \big|_{q={\rm cst}} = -\nabla \phi.\](4)

Defining \(v\) as the comoving velocity \(v := a\dot{x}\). We have two sets of coordinates \(q\) and \(x\). \(q\) being a label on a particle, telling it where it started at time \(t = 0\). Then

\[x = q + \int \frac{v}{a} {\rm d t}.\](5)

We define a momentum \(p := a^2 \dot{x} = a v\), and rewrite the factor of proportionality

\[4 \pi G \rho_u = \frac{3H_0^2 \Omega_0}{2a^3},\](6)

so that the Poisson equation becomes

\[a\nabla^2 \phi = \frac{3}{2} \Omega_m H_0^2 \delta,\](7)

and the Euler equation

\[\dot{p} = - \nabla \phi.\](8)

To this we add the Friedman equation that describes the evolution of the expansion factor

\[\dot{a} = H_0 a \sqrt{\Omega_{\Lambda} + \Omega_{m} a^{-3} + (1 - \Omega) a^{-2}}.\](9)

Note that all time dependence in these equations is in the expansion factor \(a(t)\), so we may express all time derivatives in terms of \(a\).

\[\dot{x} = \frac{p}{a^2}\quad \to \quad \partial_a x = \frac{p}{a^2 \dot{a}}\](10) \[\dot{p} = -\nabla \phi \quad \to \quad \partial_a p = - \frac{\nabla \phi}{\dot{a}}\](11)

This means we do not need to solve the Friedman equation explicitly. Rather we use \(a\) as integration variable and use the Friedman equation to determine the relevant derivative \(\dot{a}\).

The simulation

The code is structured in the following components:

• Cosmology: we need to know Hubble factor \(H\) as a function of the expansion factor \(a\).
• Mass deposition: PM codes need a way to convert from particles to a grid representation of the density.
• Interpolation: Then we need to go back and interpolate grid quantities on particle coordinates.
• Integrator: Cosmic structure formation is described by a Hamiltonian system of equations: we need to solve these, in this case using the Leap-frog method.
• Solver: To solve the Poisson equation, we need to integrate the density in Fourier space to obtain the potential.
• Initialization: The simulation is started using the Zeldovich Approximation.
• Main: glue everything together.

<<imports>>

<<cosmology>>
<<mass-deposition>>
<<mass-deposition-numba>>
<<interpolation>>
<<integrator>>
<<solver>>
<<initialization>>
<<main>>

Some things we will definitely need:

from __future__ import annotations
from dataclasses import dataclass
import numpy as np
from scipy.integrate import quad
import numba
from .cft import Box
from . import gnuplot as gp

from abc import ABC, abstractmethod
from typing import Generic, TypeVar, Callable, Tuple
from functools import partial

The Box

The Box class contains all information about the simulation box: mainly the size in pixels and the physical size it represents. All operations will assume periodic boundary conditions. In numpy this is achieved by using np.roll to shift a grid along a given axis.

Cosmology

The background cosmology is described by a function giving the scale function \(a(t)\) as a function of time. In standard Big Bang cosmology this scale function is computed from three parameters (ignoring baryons): \(H_0\) the Hubble expansion rate at \(t_0\) (\(t_0\) being now), \(\Omega_{m}\) the matter density expressed as a fraction of the critical density, and \(\Omega_{\Lambda}\) the dark energy (cosmological constant) component, again expressed as a fraction of the critical density.

@dataclass
class Cosmology:
    H0 : float
    OmegaM : float
    OmegaL : float

    <<cosmology-methods>>

From these parameters, we can compute the curvature,

\[\Omega_k = 1 - \Omega_{m} - \Omega_{\Lambda},\](12)

@property
def OmegaK(self):
    return 1 - self.OmegaM - self.OmegaL

and the (a?) gravitational constant,

\[G = \frac{3}{2} \Omega_{m} H_0^2.\](13)

@property
def G(self):
    return 3./2 * self.OmegaM * self.H0**2

The background cosmology is embodied by the Friedman equation

\[\dot{a} = H_0 a \sqrt{\Omega_{\Lambda} + \Omega_{m} a^{-3} + (1 - \Omega) a^{-2}}.\](14)

def da(self, a):
    return self.H0 * a * np.sqrt(
              self.OmegaL \
            + self.OmegaM * a**-3 \
            + self.OmegaK * a**-2)

Later on we will need the growing mode solution for this universe.

\[D(t) = H(t) \int_0^t \frac{{\rm d} t'}{a(t')^2 H(t')^2}\](15)

We’d like to do the integration in terms of \(a\), substituting \({\rm d}t = {\rm d}a/\dot{a}\).

\[D(a) = \frac{\dot{a}}{a} \int_0^a \frac{{\rm d}a}{\dot{a}^3}\](16)

For all cases that we’re interested in, we can integrate this equation directly to obtain the growing mode solution. We cannot start the integration from \(a=0\), but in the limit of \(a \to 0\), we have that \(D_{+} \approx a\).

def growing_mode(self, a):
    if isinstance(a, np.ndarray):
        return np.array([self.growing_mode(b) for b in a])
    elif a <= 0.001:
        return a
    else:
        return self.factor * self.adot(a)/a \
            * quad(lambda b: self.adot(b)**(-3), 0.00001, a)[0] + 0.00001

Using this, we can define two standard cosmologies, ΛCDM and Einstein-de Sitter.

LCDM = Cosmology(68.0, 0.31, 0.69)
EdS = Cosmology(70.0, 1.0, 0.0)

Mass deposition

To do the mass deposition, that is, convert the position of particles into a 2D mesh of densities, we use the cloud-in-cell method. Every particle is smeared out over its four nearest neighbours, weighted by the distance to each neighbour. This principle is similar (but inverse) to a linear interpolation scheme: we compute the integer index of the grid-cell the particle belongs to, and use the floating-point remainder to compute the fractions in all the four neighbours. In this case however, we abuse the histogram2d function in numpy to do the interpolation for us.

def md_cic(B: Box, X: np.ndarray) -> np.ndarray:
    """Takes a 2*M array of particle positions and returns an array of shape
    `B.shape`. The result is a density field computed by cloud-in-cell method."""
    f  = X - np.floor(X)

    rho = np.zeros(B.shape, dtype='float64')
    rho_, x_, y_ = np.histogram2d(X[:,0]%B.N, X[:,1]%B.N, bins=B.shape,
                        range=[[0, B.N], [0, B.N]],
                        weights=(1 - f[:,0])*(1 - f[:,1]))
    rho += rho_
    rho_, x_, y_ = np.histogram2d((X[:,0]+1)%B.N, X[:,1]%B.N, bins=B.shape,
                        range=[[0, B.N], [0, B.N]],
                        weights=(f[:,0])*(1 - f[:,1]))
    rho += rho_
    rho_, x_, y_ = np.histogram2d(X[:,0]%B.N, (X[:,1]+1)%B.N, bins=B.shape,
                        range=[[0, B.N], [0, B.N]],
                        weights=(1 - f[:,0])*(f[:,1]))
    rho += rho_
    rho_, x_, y_ = np.histogram2d((X[:,0]+1)%B.N, (X[:,1]+1)%B.N, bins=B.shape,
                        range=[[0, B.N], [0, B.N]],
                        weights=(f[:,0])*(f[:,1]))
    rho += rho_

    return rho

Numba implementation

It may be more efficient to do the mass deposition using Numba.

@numba.jit
def md_cic_2d(shape: Tuple[int], pos: np.ndarray, tgt: np.ndarray):
    for i in range(len(pos)):
        idx0, idx1 = int(np.floor(pos[i,0])), int(np.floor(pos[i,1]))
        f0, f1     = pos[i,0] - idx0, pos[i,1] - idx1
        tgt[idx0 % shape[0], idx1 % shape[1]] += (1 - f0) * (1 - f1)
        tgt[(idx0 + 1) % shape[0], idx1 % shape[1]] += f0 * (1 - f1)
        tgt[idx0 % shape[0], (idx1 + 1) % shape[1]] += (1 - f0) * f1
        tgt[(idx0 + 1) % shape[0], (idx1 + 1) % shape[1]] += f0 * f1

Interpolation

To read a value from a grid, given a particle position, we need to interpolate. This routine performs linear interpolation on the grid.

class Interp2D:
    "Reasonably fast bilinear interpolation routine"
    def __init__(self, data):
        self.data = data
        self.shape = data.shape

    def __call__(self, x):
        X1 = np.floor(x).astype(int) % self.shape
        X2 = np.ceil(x).astype(int) % self.shape
        xm = x % 1.0
        xn = 1.0 - xm

        f1 = self.data[X1[:,0], X1[:,1]]
        f2 = self.data[X2[:,0], X1[:,1]]
        f3 = self.data[X1[:,0], X2[:,1]]
        f4 = self.data[X2[:,0], X2[:,1]]

        return  f1 * xn[:,0] * xn[:,1] + \
                f2 * xm[:,0] * xn[:,1] + \
                f3 * xn[:,0] * xm[:,1] + \
                f4 * xm[:,0] * xm[:,1]

def gradient_2nd_order(F, i):
    return   1./12 * np.roll(F,  2, axis=i) - 2./3  * np.roll(F,  1, axis=i) \
           + 2./3  * np.roll(F, -1, axis=i) - 1./12 * np.roll(F, -2, axis=i)

Leap-frog integrator

The Leap-frog method is a generic method for solving Hamiltonian systems. We divide the integration into a kick and drift stage. In the Leap-frog method, the kicks happen in between the drifts.

It is nice to write this part of the program in a formal way. We define an abstract Vector type, which will store the position and momentum variables.

class VectorABC(ABC):
    @abstractmethod
    def __add__(self, other: Vector) -> Vector:
        raise NotImplementedError

    @abstractmethod
    def __rmul__(self, other: float) -> Vector:
        raise NotImplementedError

VectorABC.register(np.ndarray)

Vector = TypeVar("Vector", bound=VectorABC)

Given a Vector type, we define the State to be the combination of position, momentum and time (due to FRW dynamics on the background, the system is time dependent).

@dataclass
class State(Generic[Vector]):
    time : float
    position : Vector
    momentum : Vector

    <<state-methods>>

We may manipulate the State in three ways: kick, drift or wait. Kicking the state means changing the momentum by some amound, given by the momentum equation. Drifting means changing the position following the position equation. Waiting simply sets the clock forward.

def kick(self, dt: float, h: HamiltonianSystem[Vector]) -> State[Vector]:
    self.momentum += dt * h.momentumEquation(self)
    return self

def drift(self, dt: float, h: HamiltonianSystem[Vector]) -> State[Vector]:
    self.position += dt * h.positionEquation(self)
    return self

def wait(self, dt: float) -> State[Vector]:
    self.time += dt
    return self

The combination of a position and momentum equation is known as a Hamiltonian system:

class HamiltonianSystem(ABC, Generic[Vector]):
    @abstractmethod
    def positionEquation(self, s: State[Vector]) -> Vector:
        raise NotImplementedError

    @abstractmethod
    def momentumEquation(self, s: State[Vector]) -> Vector:
        raise NotImplementedError

A Solver is a function that takes a Hamiltonian system, an initial state and returns a final state. A Stepper translates one state to the next. The HaltingCondition is function of the state that determines when to stop integrating.

Solver = Callable[[HamiltonianSystem[Vector], State[Vector]], State[Vector]]
Stepper = Callable[[State[Vector]], State[Vector]]
HaltingCondition = Callable[[State[Vector]], bool]

Now we have the tools in hand to give a very consise definition of the Leap-frog integrator, namely: kick dt – wait dt/2 – drift dt – wait dt/2.

def leap_frog(dt: float, h: HamiltonianSystem[Vector], s: State[Vector]) -> State[Vector]:
    return s.kick(dt, h).wait(dt/2).drift(dt, h).wait(dt/2)

From the integrator we can construct a Stepper function (step = partial(leap_frog, dt, system)), that we can iterate until completion. After each step, the current state is saved to a file.

def iterate_step(step: Stepper, halt: HaltingCondition, init: State[Vector]) -> State[Vector]:
    state = init
    while not halt(state):
        state = step(state)
        fn = 'data/x.{0:05d}.npy'.format(int(round(state.time*1000)))
        with open(fn, 'wb') as f:
            np.save(f, state.position)
            np.save(f, state.momentum)
    return state

Poisson solver

Now for the hardest bit. We need to solve the Poisson equation.

class PoissonVlasov(HamiltonianSystem[np.ndarray]):
    def __init__(self, box, cosmology, particle_mass, live_plot=False):
        self.box = box
        self.cosmology = cosmology
        self.particle_mass = particle_mass
        self.delta = np.zeros(self.box.shape, dtype='f8')
        if live_plot:
            self._g = gp.Gnuplot(persist=True)
            self._g("set cbrange [0.2:50]", "set log cb", "set size square",
                    "set xrange [0:{0}] ; set yrange [0:{0}]".format(box.N))
            self._g("set term x11")
        else:
            self._g = False

    <<position-equation>>
    <<momentum-equation>>

The position equation:

\[\partial_a x = \frac{p}{a^2 \dot{a}}\](17)

def positionEquation(self, s: State[np.ndarray]) -> np.ndarray:
    a = s.time
    da = self.cosmology.da(a)
    return s.momentum / (s.time**2 * da)

The momentum equation:

\[\partial_a p = -\frac{1}{\dot{a}} \nabla \Phi,\](18)

where

\[\nabla^2 \Phi = \frac{G}{a} \delta.\](19)

We first compute \(\delta\) using the cloud-in-cell mass deposition md_cic() function. Then we integrate twice by method of Fourier transform. To compute the accelleration we take the second-order approximation of the gradient function.

def momentumEquation(self, s: State[np.ndarray]) -> np.ndarray:
    a = s.time
    da = self.cosmology.da(a)
    x_grid = s.position / self.box.res
    self.delta.fill(0.0)
    md_cic_2d(self.box.shape, x_grid, self.delta)
    self.delta *= self.particle_mass
    self.delta -= 1.0

    assert abs(self.delta.mean()) < 1e-6, "total mass should be normalised"

    if self._g:
        self._g(gp.plot_data(gp.array(self.delta.T+1, "t'' w image")))
    delta_f = np.fft.fftn(self.delta)
    kernel = cft.Potential()(self.box.K)
    phi = np.fft.ifftn(delta_f * kernel).real * self.cosmology.G / a
    acc_x = Interp2D(gradient_2nd_order(phi, 0))
    acc_y = Interp2D(gradient_2nd_order(phi, 1))
    acc = np.c_[acc_x(x_grid), acc_y(x_grid)] / self.box.res
    return -acc / da

The Zeldovich Approximation

To bootstrap the simulation, we need to create a set of particles and assign velocities. This is done using the Zeldovich Approximation.

def a2r(B, X):
    return X.transpose([1,2,0]).reshape([B.N**2, 2])

def r2a(B, x):
    return x.reshape([B.N, B.N, 2]).transpose([2,0,1])

class Zeldovich:
    def __init__(self, B_mass: Box, B_force: Box, cosmology: Cosmology, phi: np.ndarray):
        self.bm = B_mass
        self.bf = B_force
        self.cosmology  = cosmology
        self.u = np.array([-gradient_2nd_order(phi, 0),
                           -gradient_2nd_order(phi, 1)]) / self.bm.res

    def state(self, a_init: float) -> State[np.ndarray]:
        X = a2r(self.bm, np.indices(self.bm.shape) * self.bm.res + a_init * self.u)
        P = a2r(self.bm, a_init * self.u)
        return State(time=a_init, position=X, momentum=P)

    @property
    def particle_mass(self):
        return (self.bf.N / self.bm.N)**self.bm.dim

The main function

if __name__ == "__main__":
    from . import cft

    N = 256
    B_m = Box(2, N, 50.0)

    A = 10
    seed = 4
    Power_spectrum = cft.Power_law(-0.5) * cft.Scale(B_m, 0.2) * cft.Cutoff(B_m)
    phi = cft.garfield(B_m, Power_spectrum, cft.Potential(), seed) * A

    force_box = cft.Box(2, N*2, B_m.L)
    za = Zeldovich(B_m, force_box, EdS, phi)
    state = za.state(0.02)
    system = PoissonVlasov(force_box, EdS, za.particle_mass, live_plot=True)
    stepper = partial(leap_frog, 0.02, system)
    iterate_step(stepper, lambda s: s.time > 4.0, state)

Constrained fields

The nbody.cft library computes Gaussian random fields, and you can specify constraints on these fields.

Plotting the phase-space submanifold

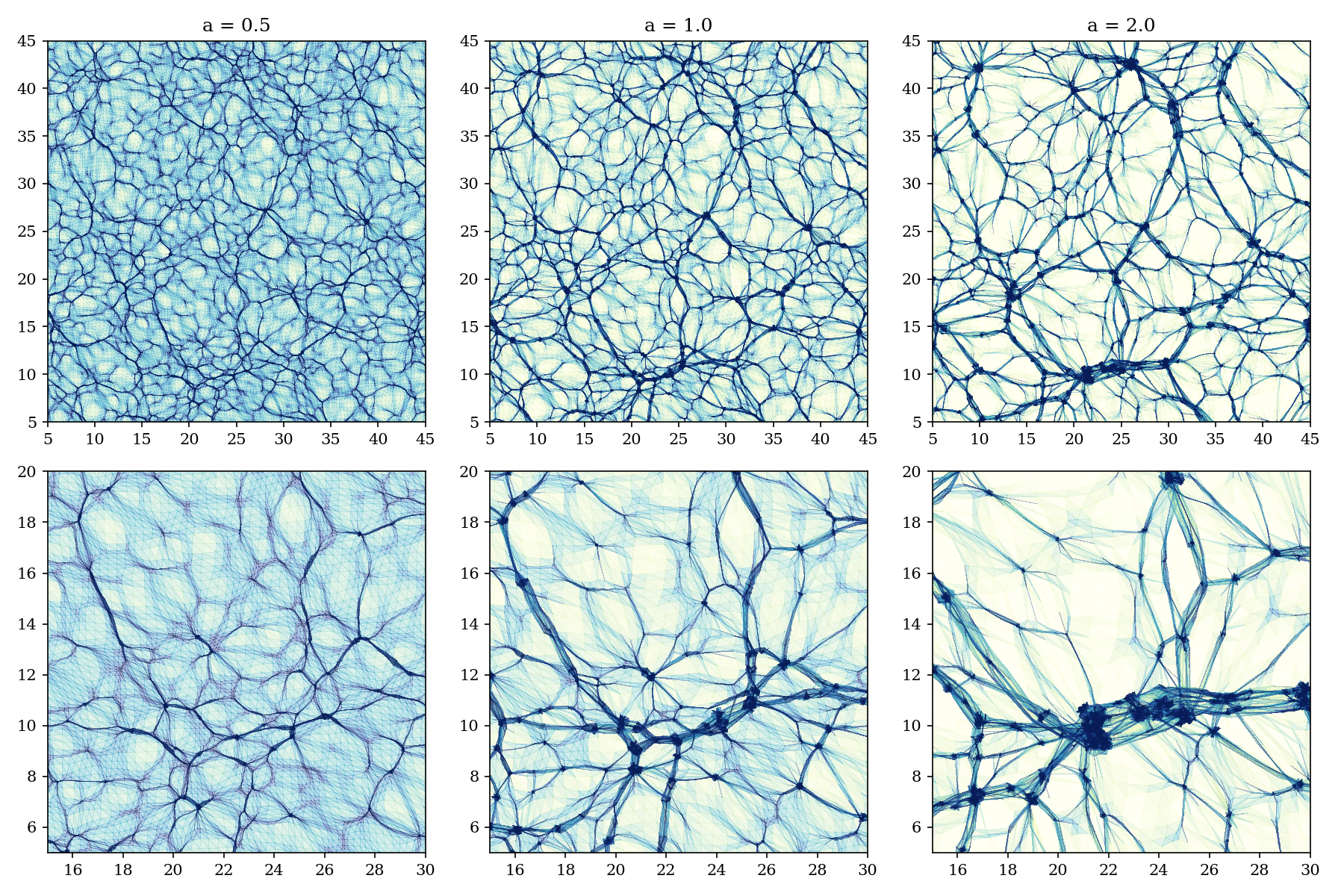
Instead of plotting particles, it is very nice to see the structures from phase-space. We take the original ordering of the particles at time \(a=0\), and triangulate that. Then we plot this triangulation as it folds and wrinkles when particles start to move.

For this visualisation we use Matplotlib.

The triangulation

We split each grid volume cell into two triangles (upper and lower). The box_triangles function generates all triangles for a given Box. In this case we don’t wrap around the edges, since that would make plotting a bit awkward.

def box_triangles(box):
    idx = np.arange(box.size, dtype=int).reshape(box.shape)

    x0 = idx[:-1,:-1]
    x1 = idx[:-1,1:]
    x2 = idx[1:,:-1]
    x3 = idx[1:,1:]
    upper_triangles = np.array([x0, x1, x2]).transpose([1,2,0]).reshape([-1,3])
    lower_triangles = np.array([x3, x2, x1]).transpose([1,2,0]).reshape([-1,3])
    return np.r_[upper_triangles, lower_triangles]

Density

To compute the density on the triangulation we take the inverse of each triangle’s area. The area of a triangle can be computed using the formula,

\[A = \frac{1}{2}(x_1 y_2 + x_2 y_3 + x_3 y_0 - x_2 y_1 - x_3 y_2 - x_0 y_3).\](20)

def triangle_area(x, y, t):
    return (x[t[:,0]] * y[t[:,1]] + x[t[:,1]] * y[t[:,2]] + x[t[:,2]] * y[t[:,0]] \
          - x[t[:,1]] * y[t[:,0]] - x[t[:,2]] * y[t[:,1]] - x[t[:,0]] * y[t[:,2]]) / 2

Plotting

The plot_for_time function reads the data from the previously saved .npy file and plots the phase-space triangulation. Note that we need to sort the triangles on their density, so that the most dense triangles are plotted last.

def plot_for_time(box, triangles, time, bbox=[(5,45), (5,45)], fig=None, ax=None):
    fn = 'data/x.{0:05d}.npy'.format(int(round(time*1000)))
    with open(fn, "rb") as f:
        x = np.load(f)
        p = np.load(f)

    area = abs(triangle_area(x[:,0], x[:,1], triangles)) / box.res**2
    sorting = np.argsort(area)[::-1]

    if ax is None:
        fig, ax = plt.subplots(1, 1, figsize=(8,8))

    ax.tripcolor(x[:,0], x[:,1], triangles[sorting], np.log(1./area[sorting]),
                  alpha=0.3, vmin=-2, vmax=2, cmap='YlGnBu')
    ax.set_xlim(*bbox[0])
    ax.set_ylim(*bbox[1])
    return fig, ax

Main script

from matplotlib import pyplot as plt
from matplotlib import rcParams

import numpy as np
from nbody.cft import Box

rcParams["font.family"] = "serif"

<<create-triangulation>>
<<triangle-area>>
<<phase-space-plot>>

if __name__ == "__main__":
    box = Box(2, 256, 50.0)
    triangles = box_triangles(box)

    fig, axs = plt.subplots(2, 3, figsize=(12, 8))

    for i, t in enumerate([0.5, 1.0, 2.0]):
        plot_for_time(box, triangles, t, fig=fig, ax=axs[0,i])
        axs[0,i].set_title(f"a = {t}")

    for i, t in enumerate([0.5, 1.0, 2.0]):
        plot_for_time(box, triangles, t, bbox=[(15,30), (5, 20)], fig=fig, ax=axs[1,i])

    fig.tight_layout()
    fig.savefig('docs/figures/x.collage.png', dpi=150)

Introducing Constrained Fields

Constraint Gaussian Random Fields are an important tool to manipulate initial conditions, while making sure that resulting fields still follow the underlying correlation function, keeping an eye on the probability of such conditions arising within a certain volume. The algorithm used here was delevoped by Hoffman and Ribak (1991); a more complete overview and applications are found in Van de Weygaert and Bertschinger (1996).

What do we know about GRFs? We have a one-point function of

\[\mathcal{P}(f_1) = \frac{1}{\sqrt{\tau v}} \exp \left[-\frac{f_1}{2v}\right]\]

and an \(N\)-point function of

\[\mathcal{P}(f) = \frac{1}{\sqrt{\tau^N \det M}} \exp\left[-\frac{1}{2}f^{\dagger}M^{-1}f\right],\]

where \(f\) is now an \(N\)-vector of values, and \(M\) the \((N \times N)\)-covariance-matrix,

\[M_{ij} = \langle f_i^*f_j\rangle.\]

In the case of Gaussian random fields, all the \(N\)-point functions can be described in terms of the two-point function, and we can write the covariance matrix as

\[M_{(2)} = \begin{pmatrix} v & \xi \\ \xi & v \end{pmatrix},\]

where \(\xi\) is the two-point correlation function. In the paper by (Van de Weygaert and Bertschinger 1996), the \(N\)-point function is written in a functional form. We will be focussing on the computation of CGRFs, we will keep the matrix the notation for finite \(N\). Computing the expectation value of a quantity \(A(f)\),

\[\langle A\rangle = \int A(f) \mathcal{P}(f) {\rm d}^N f,\] assuming \(\mathcal{P}(f)\) is properly normalised.

To show the difference between an uncorrelated and correlated random field, I have created three instances of a GRF below with power spectrum of \(P(k) = k^{n}\), where \(n = 0, -1, -2\). The value in each cell is an element in the vector \(f\).

Constraints

We will influence the generating of a random field by imposing constraints. For example, we might want a density peak in the center of our box, then we can encode this wish in a series of constraints: scaled with a certain gaussian filter the gradient is zero, and the density has some positive value, while the second derivatives are all negative. The field is then subject to a set of \(M\) constraints such that,

\[\Gamma = \left\{ C_i(f) = g_i ; i = 1, \dots, M \right\}.\]

For practical purposes we have to make sure that each costraint function \(C_i\) is linear in the sense that it can be expressed in terms of a linear combination of all elements in \(f,\)

\[C_i(f) = \langle\mathcal{C}_i, f\rangle,\]

or if you will, there is a matrix \(N \times M\) matrix \(C\) that transforms \(f\), to the set of constraint values \(g\).

In particular the case where the constraint can be expressed as a convolution is common

\[C_i(f, x) = \frac{1}{N}\sum_i g(x - y_i) f(y_i).\]

The problem is how to sample the possible constraint realisations properly,

\[\mathcal{P}\big(f|\Gamma\big) = \frac{\mathcal{P}\big(f \cap \Gamma\big)}{\mathcal{P} \big(\Gamma\big)} = \frac{\mathcal{P}\big(f\big)}{\mathcal{P}\big(\Gamma\big)}.\]

Since the coefficients \(c_i\) are linear combinations of Gaussian variables, they are themselves distributed as a multivariate Gaussian with the covariance matrix \(Q_{ij} = \langle g_i^* g_j\rangle = CMC^{\dagger},\) (how do we show this last equality? \((AB)^{-1} = B^{-1}A^{-1}\) then substitute in \(N\)-point distribution)

\[\mathcal{P}\big(\Gamma\big) = \frac{1}{\sqrt{\tau^M \det Q}} \exp\left[-\frac{1}{2}g^{\dagger}Q^{-1}g\right].\]

\[\mathcal{P}\big(f|\Gamma\big) = \sqrt{\frac{\tau^M \det Q}{\tau^N \det M}} \exp\left[-\frac{1}{2}\left(f^{\dagger}M^{-1}f - g^{\dagger}Q^{-1}g\right)\right]\]

The term in the exponential can be written in the form \(1/2F^{\dagger} M^{-1} F\), where \(F = f - \bar{f}\). Defining \(\bar{f}\), the mean field under the constraints as

\[\bar{f} := MC^{\dagger}Q^{-1}g = \big\langle f | \Gamma \big\rangle.\]

The combination \(MC^{\dagger}\) equals the cross-correlation between the random field and the set of constraints \(\langle f C_i(f)\rangle\). If we were to substitute \(C^{-\dagger}M^{-1}C^{-1}\) into this definition, we would get the expression \(C^{-1} g\), but \(C\) is in general not invertible. According to Bertschinger (1987) (B87), \(f = \bar{f}\) is a stationary point of the action: \(\delta S/\delta f = 0\) for \(f = \bar{f}\). Where the action \(S\) is the term in the exponential of the distribution function. This computation is apparently explained in Bardeen et al. (1986) (BBKS).

Moving back to WB96 and its appendix C, we now see that the constrained field is the sum of an average part \(\bar{f}\) and a residual part \(F\). The insight needed is that an unconstrained field \(\tilde{f}\) will have non-zero constraint coefficients \(\tilde{g} = C\tilde{f}\). Since everything is linear, all we need to do is add to the unconstrained field an average field with coefficients \(g - \tilde{g}\). Suppose there are two sets of constraints \(\Gamma_1\) and \(\Gamma_2\), and we have a realisation \(f_1\) with constraint coefficients \(g_1 = C f_1\), then we can transform this realisation into \(f_2\) with \(g_2 = C f_2\) as follows

\[f_2 = f_1 - \bar{f}_1 + \bar{f}_2.\]

This implies that there is a bijection between the realisations of two sets of constraints. In other words, for each realisation \(f\), drawn from the distribution with constraints \(\Gamma_1\), there is one with equal probability from \(\Gamma_2\), or

\[\mathcal{P}\big(f_1 | \Gamma_1\big) = \mathcal{P}\big(f_2 | \Gamma_2\big).\]

This also means that the residual field \(F\) is independent of the chosen constraint coefficients.

Computing the average field seems like a lot of work, since there is the matrix \(M\) in the expression. However, if we do all our work in Fourier space, the different modes \(\hat{f}(k)\) are independent, and \(M\) is diagonal. Again, because the Fourier transformation is linear, we retain all nice properties that we just derived.

References